chaos-theory

Lorenz Attractor

The Lorenz attractor is a mathematical model that describes the behavior of a chaotic system. It was discovered by Edward Lorenz in 1963 while studying atmospheric convection patterns. The attractor is defined by a set of three coupled nonlinear differential equations, which represent simplified dynamics of convection.

The Lorenz attractor is famous for its intricate and non-repeating pattern of trajectories in three-dimensional space. It exhibits sensitive dependence on initial conditions, meaning even small changes in the starting conditions can lead to significantly different outcomes. The attractor forms a butterfly-shaped structure with two symmetric but not identical wings, known as a strange attractor.

Mathematical model

This model is defined by a set of three coupled ordinary differential equations that represent the evolution of a system in three-dimensional space. These equations describe how the system’s variables change over time, determining the trajectory of the system in what is known as phase space.

Equations

The equations that govern the Lorenz Attractor are as follows:

$\frac{dx}{dt} = \sigma(y - x)$

$\frac{dy}{dt} = x(\rho - z) - y$

$\frac{dz}{dt} = xy - \beta z$

The equations define how the variables change over time, determining the trajectory of the system in phase space. Here, $x$, $y$, and $z$ represent the system’s variables, and $t$ represents time.

Parameters

The parameters $\sigma$, $\rho$, and $\beta$ are positive constants and control the dynamics of the system and can lead to various phenomena.

• Sigma (σ): This parameter represents the Prandtl number, which measures the ratio of momentum diffusivity to thermal diffusivity. Increasing or decreasing sigma affects the rate at which heat is transferred in the system.

  • When sigma is small, the system tends to be less chaotic, and the attractor may have a simpler shape with narrower lobes and fewer details.
  • As sigma increases, the attractor becomes more complex, with wider lobes, more intricate structures, and a greater range of trajectories.
  • At very high values of sigma, the system can exhibit multiple smaller attractors or even lose its chaotic behavior altogether, converging to a stable equilibrium point.

• Rho (ρ): This parameter represents the Rayleigh number, which measures the intensity of thermal convection in the system. Changing rho alters the convection and heat exchange processes.

  • At low values of rho, the system is relatively stable and may exhibit periodic or quasi-periodic behavior, with the attractor forming closed loops or torus-like structures.
  • As rho increases beyond a certain critical value, the attractor transitions into chaotic behavior, characterized by sensitive dependence on initial conditions and the formation of the well-known butterfly-shaped attractor.
  • Further increasing rho causes the attractor to undergo stretching and folding, resulting in more intricate patterns and a wider range of trajectories.

• Beta (β): This parameter represents the ratio of the width of the convection cell to its height. Changing beta influences the aspect ratio of the system.

  • For low values of beta, the attractor remains similar to the standard Lorenz attractor, with the characteristic butterfly shape.
  • Increasing beta leads to a change in the attractor’s structure. The lobes become elongated and stretched along a specific direction, distorting the butterfly shape.
  • Very high values of beta can cause the attractor to become more symmetric, with the lobes expanding and appearing more rounded.

Characteristics

The Lorenz Attractor exhibits several key properties of chaotic systems. One of the most notable properties is its sensitive dependence on initial conditions. Even tiny variations in the initial values of x, y, and z can lead to vastly different trajectories and outcomes over time. This sensitivity is a hallmark of chaos and reflects the exponential amplification of small differences.

Another important characteristic of the Lorenz Attractor is the presence of a strange attractor. The trajectory of the system never repeats itself, and it settles into a complex, non-repeating pattern. The attractor has a fractal nature, meaning that it exhibits self-similarity at different scales. When visualized, the Lorenz Attractor reveals intricate details and fine structures that repeat at different levels of magnification.

Code features

• Ability to rotate, zoom in and zoom out the camera (dragging and scrolling).
• Change value for sigma parameter ($\sigma$, s key with SHIFT as modifier).
• Change value for rho parameter ($\rho$, r key with SHIFT as modifier).
• Change value for beta parameter ($\beta$, b key with SHIFT as modifier).
• Change value for time expansion ($dt$, t key with SHIFT as modifier).
• Clear window on command (c key).
• Change between trajectory and point-only modes (m key).

Dependencies

In the root directory of the project all CMakeLists files are included, you just have to rename the one you need to use to CMakeLists.txt.

Linux

Install the required libraries using the following commands:

sudo apt install build-essential
sudo apt install libglew-dev
sudo apt install libglfw3-dev
sudo apt install libglm-dev
sudo apt install libassimp-dev
sudo apt install libfreeimage-dev

MacOS

Install the required libraries using the following commands:

brew install gcc
brew install glew
brew install glfw
brew install glm
brew install assimp
brew install freeimage

Windows

All the required libraries are including in the /lib/ directory.

Also, you might need MinGW, in case you do not have it already installed. You can download it from OSDN website.

Experiments

Experiment 1

Parameters: $\sigma = 10$, $\rho = 28$, $\beta = 8/3$:

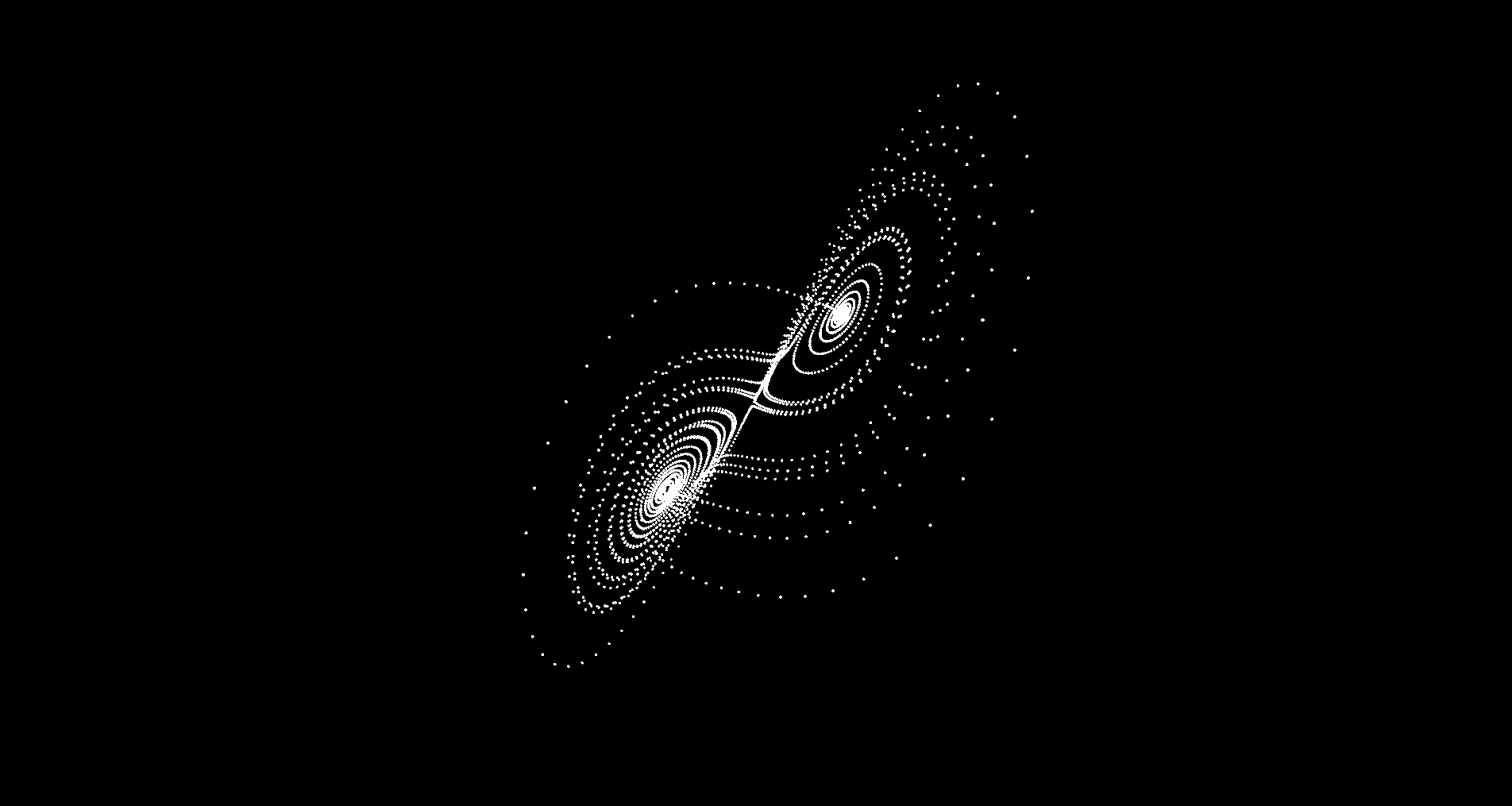
Experiment 2

Parameters: $\sigma = 10$, $\rho = 50$, $\beta = 4$:

Experiment 3

Parameters: $\sigma = 10$, $\rho = 45$, $\beta = 10$:

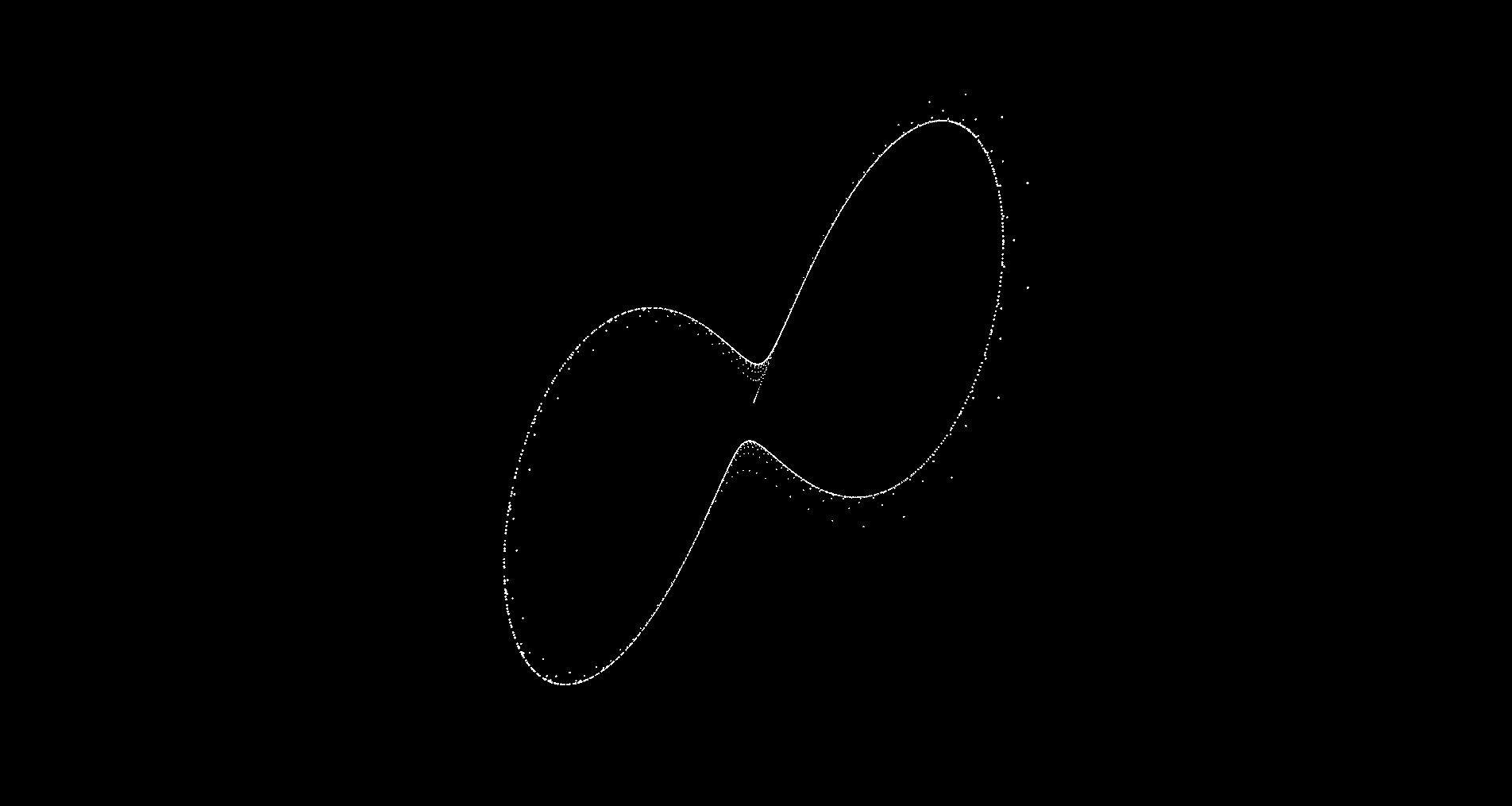
Experiment 4

Parameters: $\sigma = 25$, $\rho = 40$, $\beta = 7$:

Experiment 5

Parameters: $\sigma = 5$, $\rho = 15$, $\beta = 2$:

Conlcusion

In conclusion, the implementation of the Lorenz attractor model provides a valuable tool for studying and visualizing the dynamics of a chaotic system. The Lorenz attractor is a well-known example of a chaotic system and is widely used to illustrate the principles of chaos theory.

By implementing the Lorenz attractor model, users can generate time series data that captures the complex behavior of the system. This data can be further analyzed and visualized, allowing for a deeper understanding of chaotic phenomena such as sensitivity to initial conditions, strange attractors, and the intricate patterns of trajectories.

The implementation of the Lorenz attractor model offers the opportunity to explore different parameter settings, such as sigma, rho, and beta, and observe the resulting changes in the attractor’s structure and behavior. This allows users to gain insights into how variations in these parameters affect the system’s chaotic dynamics.

Furthermore, the visualization capabilities provided by the implementation allow users to observe the attractor’s geometric shape and its evolution over time. This visual representation enhances the intuitive understanding of chaotic behavior and provides a platform for further analysis and exploration.

Overall, the implementation of the Lorenz attractor model serves as a powerful tool for studying chaos theory, promoting experimentation, and advancing the understanding of chaotic systems and their implications in various fields of science and engineering.

This site is open source. Improve this page.